문제
[문제 설명]
로봇이 m x n 격자에 있습니다. 로봇은 초기 위치에서 왼쪽 상단 모서리(즉, grid[0][0])에 있습니다.
로봇은 오른쪽 하단 모서리(즉, grid[m-1][n-1])로 이동하려고 합니다.
로봇은 언제든지 아래쪽이나 오른쪽으로만 이동할 수 있습니다.
정수 m과 n이 주어지면, 로봇이 오른쪽 하단 모서리에 도달하기 위해 취할 수 있는 가능한 고유 경로의 수를 반환하세요.
테스트 케이스는 정답이 2 * 109 이하가 되도록 생성됩니다.
[제한 사항]
1 <= m, n <= 100
[입출력 예시]
m n return
3 7 28
3 2 3
[입출력 예시 설명]
입출력 예#1
총 28가지 경로가 있습니다.
입출력 예#2
왼쪽 상단 모서리에서 오른쪽 하단 모서리로 도달하기 위한 총 3가지 경로가 있습니다
1. 오른쪽 -> 아래 -> 아래
2. 아래 -> 아래 -> 오른쪽
3. 아래 -> 오른쪽 -> 아래
문제 분석
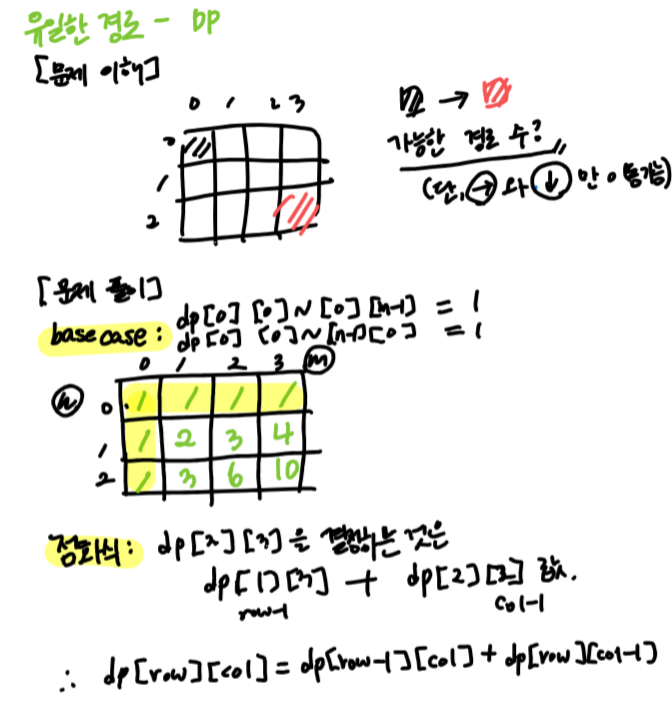
- 로봇이 좌상단 → 우하단 으로 가는 경우의 수 구하기 (이동은 오른쪽, 왼쪽으로만 가능)
- row가 0이거나 col이 0인 경우 이동할 수 있는 경우의 수는 한 개밖에 없다. (쭉 직진)
- 해당 지점의 이동 경우의 수는 해당 지점 위쪽의 이동 경우의 수 + 해당 지점의 왼쪽의 이동 경우의 수 이다.
- DP의 메모이제이션 특성을 활용하여 각 지점까지 이동할 수 있는 경우의 수를 저장한다.
정답 코드
정답 코드에서는 dp 배열 대신 board 배열로 메모이제이션을 하였다.
import java.util.*;
class Solution {
public int solution(int m, int n) {
int answer = 0;
int[][] board = new int[n][m];
for(int row=0; row<n; row++) {
for(int col=0; col<m; col++) {
if(row == 0 || col == 0) { // basecase
board[row][col] = 1;
}
else { // logic
board[row][col] = board[row-1][col] + board[row][col-1];
}
}
}
return board[n-1][m-1]; // 도착 지점까지 도착하는 경우의 수 출력
}
}
교훈점
현재 경우의 수를 구하기 위해서 이전 경우의 수를 구해야 하는 경우 매번 연산하는 것이 아니라 그 연산 결과를 저장하고 활용하여 연산 횟수를 줄일 수 있다. (메모이제이션)



