[백준] 2644 : 촌수계산 (C++)

문제

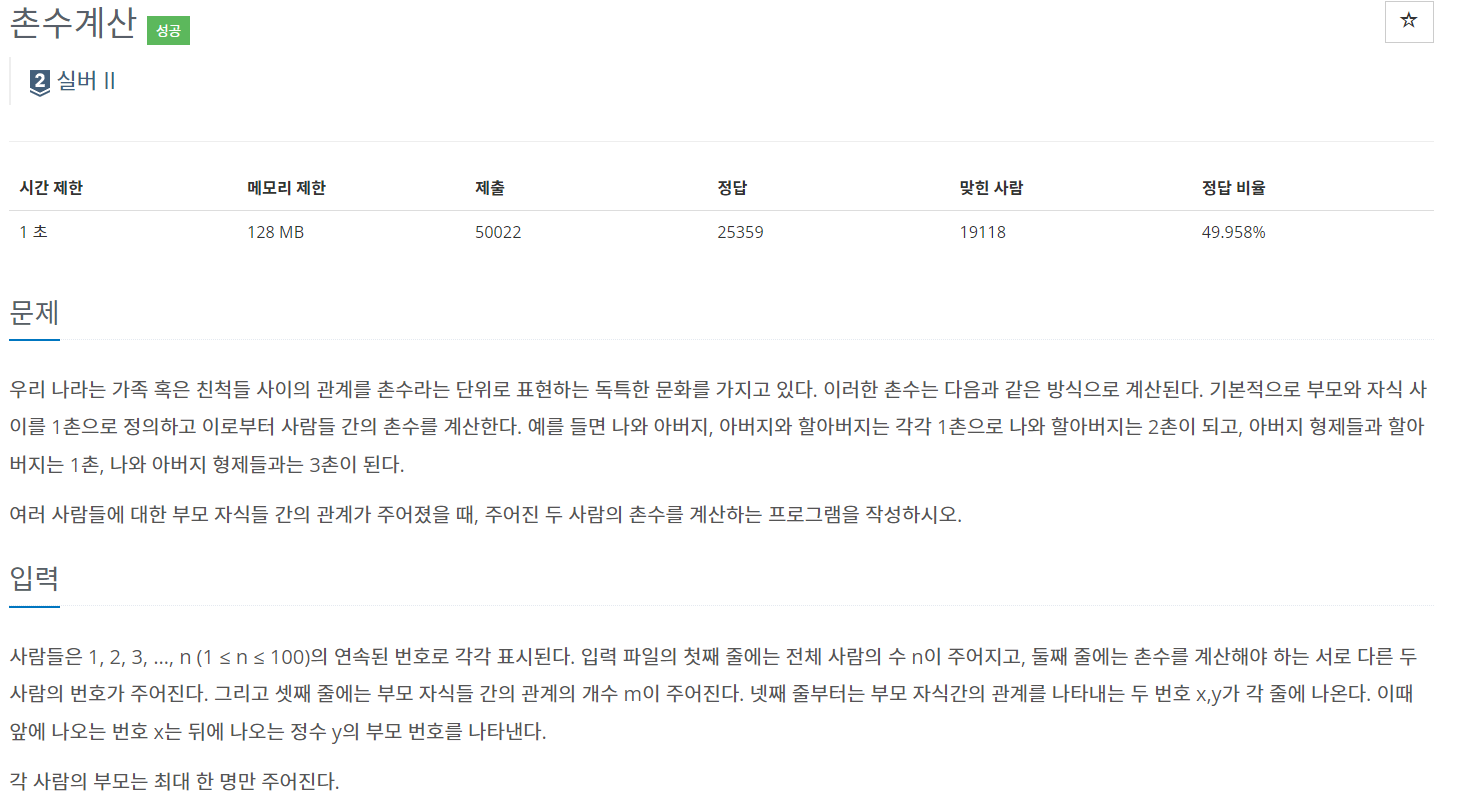
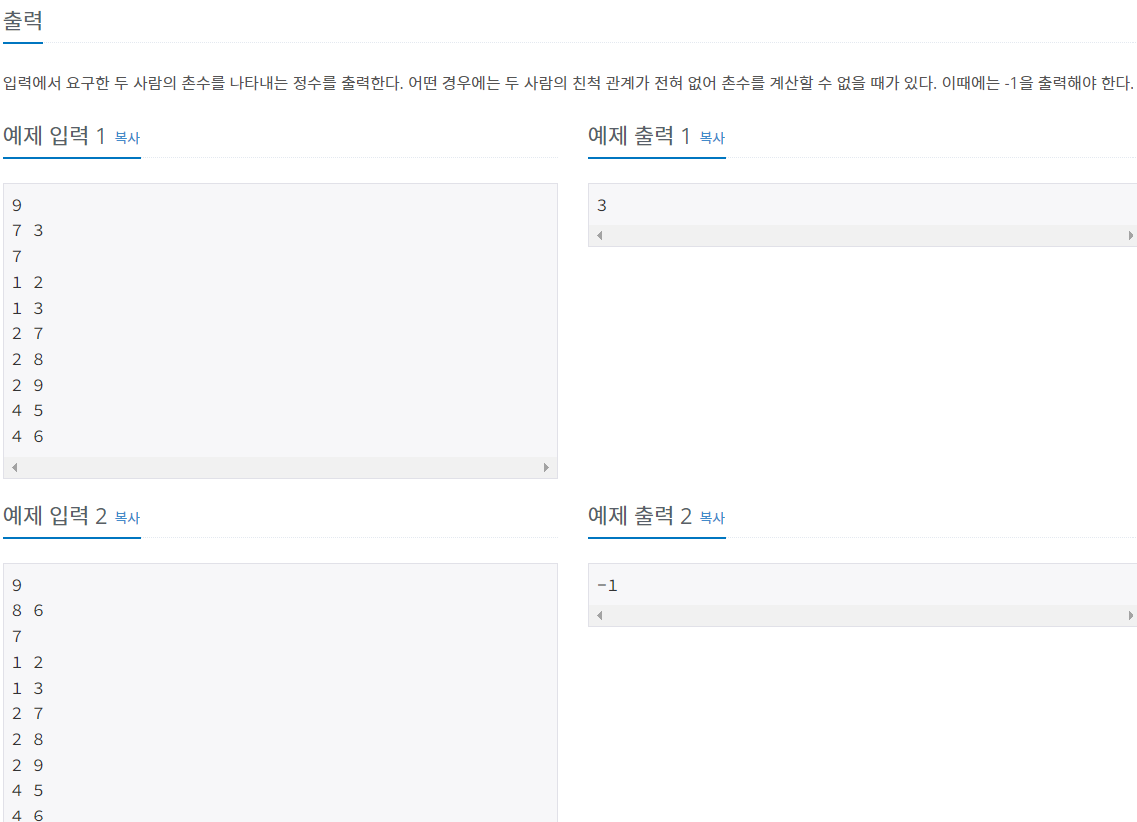
문제 분석

- 문제는 말 그대로 촌수를 계산하는 문제이다.

- 예제 입력 1을 그래프 형태로 그리면 아래 그림과 같고, 7에서 3을 찾으려면 3번 이동해야 되기 때문에 정답은 3이다.

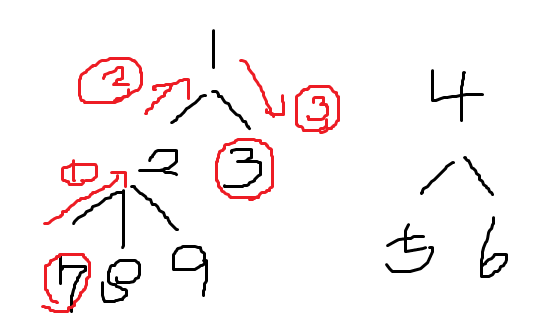
- 간선의 가중치가 동일하고(이 문제에서는 한 번 이동에 이동 횟수 1 증가) 목표 지점까지의 최단 거리를 묻는 문제이기 때문에 BFS을 사용한다.

정답 코드

// 풀이 시간 : 25분 35초
// BFS 탐색을 통해 7 3 이 입력되면 7에서부터 시작해서 3을 만날 때까지 그 거리를 구하면 된다.

#include <iostream>
#include <queue>

using namespace std;
#define MAX_N 101 // 사람들은 최대 100명

int Board[MAX_N][MAX_N];
int move_cnt[MAX_N]; // 각 노드가 도착한 최초 이동 횟수 
int n;

void bfs(int start_node, int end_node) {
	int visited[MAX_N];
	fill(visited, visited + MAX_N, 0); // 0으로 초기화
	queue<int> q;
	
	// 초기 노드 방문 처리
	q.push(start_node);
	visited[start_node] = 1;
	
	while (!q.empty()) {
		int cur_node = q.front();
		q.pop();
		if (cur_node == end_node) {
			cout << move_cnt[cur_node];
			return;
		}
		
		for (int next_node = 1; next_node <= n; next_node++) {
			if (Board[cur_node][next_node] != 1) continue; // 부모-자식 관계가 아닌 경우 패스
			if (visited[next_node] != 0) continue; // 이미 방문한 경우 패스
			
			// 연결된 다음 노드 방문 처리
			q.push(next_node);
			visited[next_node] = 1;
			move_cnt[next_node] = move_cnt[cur_node] + 1;
		}
	}
	cout << -1;
}

int main(void) {
	ios_base::sync_with_stdio(false); cin.tie(nullptr);
	cin >> n;
	int start_node, end_node;
	cin >> start_node >> end_node;
	int m;
	cin >> m;
	// 부모 - 자식 간의 관계 연결
	for (int i = 0; i < m; i++) {
		int parents, child;
		cin >> parents >> child;
		Board[parents][child] = Board[child][parents] = 1;
	}

	// 촌수 찾기
	bfs(start_node, end_node);

	return 0;
}